PlaidCTF - Crypto200 - Compression

  It's been a long time since I've blogged. I've been really busy with school and well... life in general.. as well a shift in focus. It sucks because before this weekend I can't remember the last time I actually made time for doing/learning anything sec-related. I feel like if I need a large chunks of uninterrupted free time to be able to get anything done and I just haven't had many of those chunks lately. I can't say I've been wasting time though. I've been investing a lot of time into developing my programming/problem solving skills in general ( mostly via competitive programming ) and that's always a good thing. I've been so out of the loop that I didn't even know that the Plaid CTF was starting until about an hour before it did ( so much for any kind of preparation! ). However, I can successfully say that I dedicated the vast majority of my time this weekend ( while ignoring assignments and the fact that finals are a little less than 2 weeks away) to participating in the CTF. I don't regret it at all. I can't remember the last time I've learned so much in such a short space of time and enjoyed it this much.

  I've been meaning to write something here for a while and now and I figured with me completing a few challenges in the CTF that I could do a writeup or two and see how it turns out. I mostly focused on the crypto challenges this time around. It's always been an area that I've been interested in but I've never really devoted a lot of time to so this was the perfect time; I was participating just for the fun of it and to learn, not competitively. Out of the few that I did solve, the one I enjoyed the most was the crypto200 - compression challenge. So here is my writeup :)


  The script above was provided to us for the challenge. The script in question was actually being run on one of their servers but with the PROBLEM_KEY and ENCRYPT_KEY set to their real values. From reading the comment on line 11, it becomes obvious what the goal is.

GOAL: Determine the PROBLEM_KEY

  At this point in time, the only information that we have about the problem key is that it's 20 characters long and it consists only of lowercase letters and underscores. The fact that they provided us witha charset hints towards the solution requiring some enumeration/bruteforcing.

  The next step, after determining what the goal was, was to take a closer look at the script and determine what it was doing.
Moving further down the script, the next thing we see is the encrypt function.



  Looking at the encrypt function we can see that it uses AES. A little background on that:
AES ( Advanced Encryption Standard ) is a symmetric block cipher. That just means that it operates on a fixed amount of data at a time and that it uses the same key for both encryption and decryption as opposed to asymmetric key encryption like RSA which uses different keys for encrypting and decrypting.

  Now with block ciphers, by design, they are only supposed to operate on one block of a fixed size. So what happens if there is more than one block?

Let's call our encryption function E, our key, K and we have two messages M₁ and M₂ and two ciphertexts C₁ and C₂
E_k(M₁) = C₁
E_k(M₂) = C₂

  The AES algorithm on its own is completely deterministic; for a given input ( k,M_x ) it will always produce the same output C_x. This is undesirable because it allows us to deduce something about the plaintext given the ciphertext. Just as an example( I'm not going to bother being technically accurate here ), consider that I had to encrypt the string "abccdeabcdef" and that a block size of 3 bytes was being used.

String: "abccdeabcdef"

Separated into 3 byte blocks: ["abc"]["cde"]["abc"]["def"]

  Now given that the block ["abc"] occurs twice, and the algorithm being completely deterministic, when looking at the ciphertexts for the different blocks, it will be quite noticeable that the same ciphertext occurs twice. Seeing that, we might not be able to deduce what exactly the plaintext was but we are able to deduce that whatever the plaintext was, it occurred at least twice within the string. Therefore we can deduce something about the plaintext by looking at the ciphertext and this is semantically insecure.

To combat this, when a block cipher with a particular key needs to be applied to more than one block, a mode of operation is necessary.

Taken from Wikipedia:

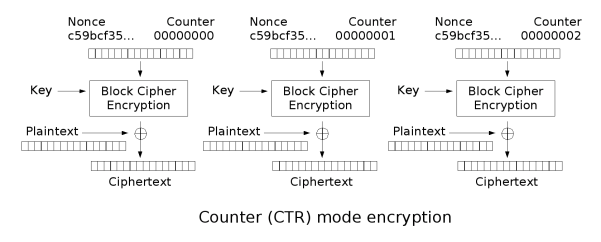
 A mode of operation describes how to repeatedly apply a cipher's single-block operation to securely transform amounts of data larger than one block.^[

  Looking at the second parameter passed to AES.new(), we see AES.MODE_CTR otherwise known as Counter. This mode of operation essentially turns the block cipher into a stream cipher. The Counter is just required to produce a sequence which is guaranteed not to repeat for a long time ( usually an increment by 1 scheme is used ). In addition to the Counter, a Cryptographic Nonce is used. The nonce is usually generated from some random generator suitable for crypto purposes. The nonce is combined with the value from the counter because of the value from the counter being predictable.

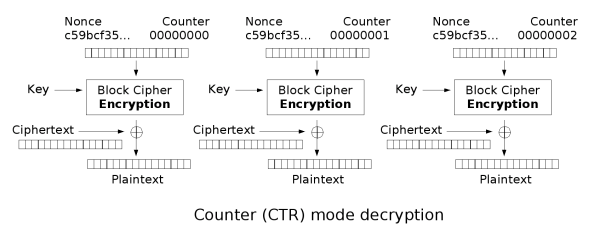
  Now instead of encrypting the actual plaintext, the combination of the nonce and the counter value is encrypted instead to form the keystream. This keystream is then combined, in this case XOR'd, with the plaintext to form the ciphertext. The two diagrams below, taken from Wikipedia, illustrate the encryption and decryption processes.

However, one thing to keep in mind is that the plaintext passed to the encrypt function is compressed before it is actually encrypted. Keeping in mind that the name of the challenge was compression, it would probably be a good thing to keep in mind.

So far we know:

• The program uses AES encryption with a 256 bit key
• It uses CTR as it's mode of operation so it can be used on multiple blocks.
• The nonce used comes from Python's os.urandom().The Python doc's state that this function is suitable for generating random bytes of data suitable for cryptographic use. 
• The PROBLEM_KEY is 20 bytes long with a charset consisting of lowercase letters and underscores.
• The plaintext is compressed before it is encrypted.

It isn't feasible to bruteforce the key. 2^256 different permutations isn't something we want to bruteforce.
It isn't feasible to bruteforce the PROBLEM_KEY. 27^20 permutations also isn't something we want to bruteforce. This naive approach is not going to work.

Moving further down the script we see:


As we connect to the server, the nonce is sent to us.

Does this help us at all?

We have the nonce and we can predict the counter values and therefore we know what's being encrypted to form the keystream. If we could figure out what the keystream was, it would be trivial to recover the plaintext. However, we don't have the AES encryption key so that isn't possible. I'm not sure why the nonce was sent but I think it was only really meant as a red herring but I could be very wrong.


Looking at the rest of the script we see mostly trivial details. The first four bytes we send to the server is interpreted as the length of the message about the follow. The server appends the PROBLEM_KEY to the data we send then first sends its length back to us followed by the encrypted version of the compressed data. The detail that really stands out here is that the PROBLEM_KEY is appended to the data.


Looking at what we have so far, it's probably not feasible to perform any sort of AES related attack. What do we have left? We know that the plaintext has the PROBLEM_KEY appended to it  before it is compressed and then encrypted.


We've already looked at the encryption so now let's take a look at the compression. The program uses the zlib library for compression. How does zlib work? A quick google search and some looking around will get you to this page which contains a sufficient explanation of the DEFLATE algorithm which zib uses. Essentially the DEFLATE algorithm uses Huffman Trees and LZ77 compression. The LZ77 compression algorithm looks for repeated substrings foward in the sequence up to a certain point and takes advantage of this redundancy. Instead of storing the same substring multiple times, at every repeated occurrence, it simply stores how far back the identical substring occurred and its length.

zlib.compress(our_data+PROBLEM_KEY) is what is taking place.

From the description of the DEFLATE algorithm, and with the knowledge of what is being compressed, it becomes clear what needs to be done. We can use the fact that the data is being compressed before it is encrypted to gather information about the plaintext and ultimately, the PROBLEM_KEY.

The length of the returned ciphertext should differ depending on how much of PROBLEM_KEY occurs in our string. Assuming that I had the first x-1 characters of the PROBLEM_KEY correct, appending the xth character would cause the length of the ciphertext take one of two values depending on whether the xth character was correct or not. The character that produced the shorter ciphertext would be the correct one.

I wrote that small script solely for the purpose of experimenting to see how the length of the compressed data varied with my input. The first thing I tried to do was to determine the first character of the PROBLEM_KEY. I realized that the compression really only started kicking in when the string I chose had all four of its characters matching the first character of the PROBEM_KEY.


After a little more experimentation, I realized that until I had at least the first four characters right I had to follow a certain pattern and from then on I could just append single characters and work with the respective lengths of the ciphertexts.

For example, if I knew c matched the first character. I would try cacacaca , cbcbcbcb, ... , c_c_c_c_ and pick the one that produced the smallest ciphertext. I did this until I had the first four characters and from there I took a much more straightforward route.

Below is the script I used to automate the process:




Now the explanation above about zlib was just a general idea of how it works. The script mostly works but it does get stuck at a few points. For instance, it successfully deduced crime_somet but another candidate string crime_some_ received the same length ciphertext and as the script continued the latter candidate moved forward while the first did not. That's the reason for me having the option to pass the first candidate as a command line argument. I had to coach the script along a bit but it did do most of the work and after about 2 pushes in the direction at the points where it started failing, it successfully produced the PROBLEM_KEY.

All that work just for "crime_sometimes_pays" :)

It was definitely an awesome challenge and I learned a lot from it. It was also a nice opportunity to brush up on my python.